La función exponencial se utiliza para describir cualquier cosa que está en continuo crecimiento. Por ejemplo, el número de células de un feto mientras se desarrolla en el útero materno, o doblar reiteradamente un papel por la mitad, donde el grosor del papel crece exponencialmente.

Cómo la leyenda del ajedrez y los granos de trigo está ya muy vista, comentaré la historia del hombre que trabaja por un céntimo al día durante un mes, pero dobla su sueldo cada día. El último día del mes estaríamos ganando más de 10 millones de euros al día. Yo me conformaría con trabajar únicamente en Febrero (3 días más corto), pero solamente estaría ganando 2,6 millones de euros, en vez de los 21 millones de Mayo. Cómo bien dice Negroponte, la parte que la gran mayoría de la gente recuerda es la de los 10 millones al día. Sin embargo:

Cuando el efecto es exponencial, esos 3 días cuentan mucho.

Aquí es cuando entra en juego una popular presentación sobre aritmética, población y energía que Harry me pasó hace un tiempo, donde el doctor en física Albert Bartlett afirma contundentemente que el mayor defecto de la raza humana es nuestra falta de habilidad para comprender la función exponencial. Pero es que en verdad, los medios no nos lo ponen fácil. Las noticias están llenas de porcentajes de crecimiento, que no son fáciles de entender:

“Las exportaciones hortofrutícolas se estancan y las importaciones crecen al 20%“. Se están utilizando cantidades de crecimiento en un tiempo constante (anualmente) que son más difíciles de interpretar que si las expresáramos en tiempo para doblarse. Veamos como Barltlett nos explica como realizar esta traducción:

Si una tasa de crecimiento anual es del 20%, supone un tiempo concreto (un año) para crecer un 20%. Eso supone que necesitaremos un tiempo mayor para crecer el 100%, que es justamente el tiempo para doblarse. El tiempo necesario para doblarse se obtienen de la siguiente manera (¡atención expresión matemática!):

Tdoblarse = 70 / % de crecimiento

Así un crecimiento del 20% requiere un tiempo necesario para doblarse de 3,5 años (70 / 20). ¡Es más fácil entender un crecimiento en tiempo para doblarse que en porcentaje de crecimiento!

Si nos propusiéramos escribir diariamente en nuestro blog, pero doblando el número de posts cada día (el segundo día 2 posts, el tercer día 4 posts, el cuarto escribiríamos 8 posts y así sucesivamente), a los 24 días tendríamos que escribir más posts que todas las entradas de la Wikipedia en todos los idiomas (10 millones).

Si nos fijamos, el crecimiento exponencial supone además que cada día en el que doblamos nuestro ritmo de publicación, estamos escribiendo más posts que todos los que había en el archivo del blog. La producción al doblarse es mayor que todas las producciones anteriores juntas.

Por esta razón, un crecimiento exponencial no es sostenible. Es imposible satisfacer la demanda final (¡escribir 10 millones de posts!). Veamos entonces que ocurre cuando el crecimiento continuo de los países desarrollados demanda los mismos niveles de energía, más concretamente de petróleo, cuya demanda actual es del 2,7% anual de crecimiento. Este ritmo de crecimiento hace que la demanda de crudo se duplique en 26 años (T_doblarse = 70 / 2,7). En ese tiempo quemaremos más petróleo que lo que nunca se ha quemado en toda la historia de la humanidad y estamos hablando de una fuente de energía no renovable y finita. Las reservas de crudo pueden agotarse en 40 años si somos optimistas, y semejantes cálculos pueden aplicarse para el gas natural, el carbón y el uranio.

Aunque en verdad, este crecimiento exponencial no toma la forma de la función exponencial, donde un día pasamos de tener todo el petróleo del mundo a pasar a “no tener ni gota”. Este modelo en ocasiones es una función logística (como en el desarrollo de un embrión, donde el número de células acaba estabilizándose para formar al adulto) o toma, como en este caso, la forma de una función gaussiana, con esa característica apariencia de campana:

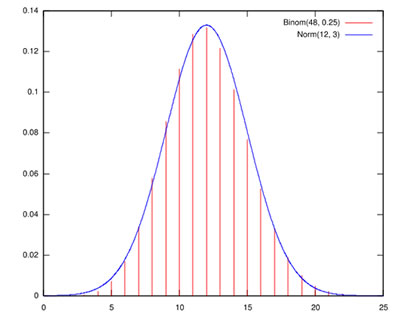
Pues bien, actualmente nos encontramos cayendo por la bajada estrella de la montaña rusa de la demanda energética. Nos encontramos cayendo por la pista roja de la estación mundial de la economía. Nos encontramos inmersos en una crisis a nivel global.

Hasta aquí no he dicho nada nuevo, pero esta crisis no es una mera recesión como puede interesar hacernos creer. Esto es un cambio global y el mañana no será como el ayer.

Continuará en… La crisis. Problema y solución (y II): la solución es menos. (practicando con el efecto Zeigarnik)